フィボナッチ数列とは
フィボナッチ数列とは第1項が1、第2項が1、第3項が第1項と第2項の和で2、第4項が第2項と第3項の和で3、第5項が第3項と第4項の和で5、第6項が・・・・と続く数列である。数列を一部書き出すと
1、1、2、3、5、8、13、21、34、55、89、・・・・・
となる。
1202年、イタリアの数学者レオナルド・フィボナッチが著書「算盤の書」でこの数列を取り上げたことからフィボナッチ数列と言われるようになった。
一般項
フィボナッチ数列は大学入試にも頻繁に出題されている。大学受験を目指す高校生にとっては重要項目である。その一般項はnを自然数として、
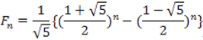
で与えられる。各項は自然数であるにも関わらず、一般項に無理数の√5 が出て来る不思議な数列である。
ひまわり
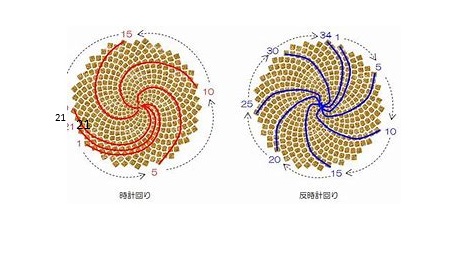
ひまわりの種は花の表面にびっしりと配置されている。中心からの種の配置は時計周りの曲線(図の赤線)と反時計周りの曲線(図の青線)の模様を描いている。時計周りの曲線の数を数えると21、反時計周りの曲線の数を数えると34である。21も34もフィボナッチ数列に表れる数である。
実はひまわりの種の曲線の配置数は、21と34、34と55、55と89の3パターンしかないのである。いずれの数字もフィボナッチ数列に表れる数である。ひまわりの花の中にできるだけたくさんの種を配置する配置の仕方はフィボナッチ数が最適の配置方法なのである。
フィボナッチ数は、植物の花びらの枚数にも表れている。
- 3枚:ユリ、アヤメ、エンレイソウ
- 5枚:オダマキ、サクラソウ、キンボウゲ、ノイバラ、ヒエンソウ
- 8枚:デルフィニウム属、サンギナリア、コスモス
- 13枚:シネラリア、コーンマリゴールド
- 21枚:チコリー、オオハンゴンソウ
- 34枚:オオバコ、シロバナムシヨケギク
- 55枚:ユウゼンギク
- 89枚:ミケルマス・デイジー
フィボナッチ螺旋
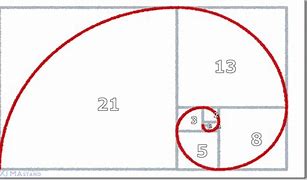
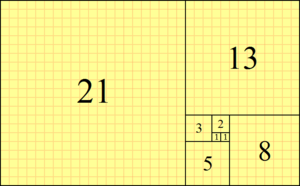
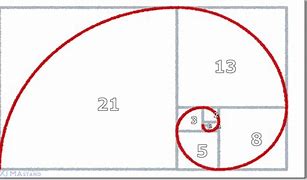
長さ1の正方形を2個横に並べて置き、その上に長さ2の正方形を置く。その左に長さ3の正方形を置き、その下に長さ5の正方形を置く。その右に長さ8の正方形を置き、その上に長さ13の正方形を置く。これを繰り返すと下図のような図形が出来上がる。こうして出来た正方形の角を曲線で結ぶと螺旋曲線が出来上がる。この螺旋はフィボナッチ螺旋と呼ばれている。
自然界には螺旋が頻繁に表れる。秋になると日本列島に甚大な被害をもたらす台風は、台風の目を中心に螺旋模様を描いている。天気予報図で雲が螺旋を描いて回転している状況が毎年テレビで放送される。螺旋が台風を安定した状態のまま維持し強力なパワーを発揮させるのだ。
また、銀河も螺旋を描いて回転している。数億個の惑星・恒星を抱え螺旋を描いて回転することにより、銀河は何十億年も銀河の形状を維持している。
これら自然界の中で存在する螺旋の中で、フィボナッチ螺旋が最も美しい螺旋であると言われている。