素数が無限にあること
紀元前のギリシャ時代から素数が無限にあることは知られていた。
その証明は、仮に素数が有限個だとして、それらを小さい順にp1、p2、p3、p4、・・・・、pnとする。 k = p1 x p2 x p3 x p4 x・・・・x pn + 1 を考える。kはpnより大きいから素数ではない。kをp1で割ると1余るからp1はkの素因数ではない。kをp2で割ると1余るからp2はkの素因数ではない。kをp3で割ると1余るからp3はkの素因数ではない。・・・・。kをpnで割ると1余るからpnはkの素因数ではない。するとkはp1、p2、p3、・・・・、pn以外の素因数を持つこととなり矛盾となる。
自然数の多さ
1、2、3、4、・・・・と続く自然数は無限にある。その大きさはどれ位であろうか。その大きさを計る手段として、数学では逆数の和をとる手法が常道である。
S(x) = 1 + 1/2 + 1/3 + 1/4 +・・・・+ 1/x
を考える。S(x) ~ logxである。f(x) ~ g(x) の意味は f(x) と g(x) は x が無限に大きくなったとき f(x) と g(x) の値がほぼ同じくなる、ということである。x 以下の自然数の逆数の和は無限大において logx と値がほぼ同じくなる。S(x) ~ logx はスイスの数学者オイラーが証明した。

素数の多さ
同じように x 以下の素数の逆数の和
T(x) = 1/2 + 1/3 + 1/5 + 1/7 + ・・・・ + 1/p ( p ≦ x , p は素数)
としたとき、T(x) ~ log(logx) である。log(logx) < logx なので素数の個数は自然数の個数より少ない、と言える。T(x) ~ log(logx) はポーランドの数学者メルテンスが証明した。
素数定理
Π(x) を x 以下の素数の個数とすると Π(x) ~ x/logx が成り立つ。 x 以下の素数の個数は無限大において x/logx とほぼ値が等しい。
Π(x) ~ x/logx は素数定理と言われ、整数論の基本定理である。ガウスがこの定理を予想し、100年後にフランス人アダマールとベルギー人ド・ラ・バレ=プーサンがそれぞれ独自に証明した。

Π(x) ~ x/logx を Π(x)/x ~ 1/logx と変形すると、左辺は1から x までの素数の個数を x で割っているので1から x までの素数の存在確率である。右辺の 1/logx は単調減少関数であるので、1から x までの素数の存在確率は減少の一途を辿ることが分かる。 x が莫大に大きな数になると、素数の存在確率は限りなく0に近くなる、と言える。
ζ(2)
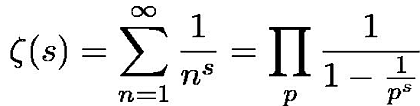
上記の関数はリーマンゼータ関数である。自然数の s 乗の無限和であると同時に素数の s 乗の無限積である。
ζ(2) = 1 + 1/4 + 1/9 + 1/16 + 1/25 +・・・・の値がいくらになるかはバーゼル問題と言われ長らく研究されて来た。オイラーが 、ζ(2) は収束しておりその値は
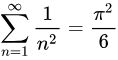
である、と証明した。
4や25など自然数の2乗の数は平方数と言われている。平方数は逆数の和が収束しているため自然数や素数より数が少ない、と言える。
リーマン予想
負の偶数点 s = ー2n ( n = 1、2、3、・・・) における ζ(s) の値は 0 である。この零点は自明な零点または実零点と呼ばれる。
ζ(s) の非自明な零点は、0 < Re(s) < 1 の領域にある。この零点は複素零点と呼ばれる。リーマン予想は、「複素零点はすべて Re(s) = 1/2 の直線上にあるだろう」というものである。1859年にドイツの数学者ベルンハルト・リーマンがこの予想を提唱してから現在まで未解決である。
素数と複素零点を対応づけてリーマン予想を証明しようとする数学者など、多数の数学者が日々リーマン予想に取り組んでいるが、未解決難問として立ちはだかっている。リーマン予想が証明されれば素数の謎が解ける、と言われている。素数がどれだけ沢山あるか、素数の分布の規則性などの素数の謎が解けるかもしれない。


