リーマン予想とゼータ関数

π(x)

上の表は、与えられた数 x 以下の素数の個数を表した表である。素数の表れるタイミングは実に不規則だ。ドイツの数学者ベルンハルト・リーマンはπ(x)を関数で表すことを考え、１８５９年の論文でπ(x)を関数で表した。その関数はゼータ関数の複素零点を使った無限和で表されるものだった。

ゼータ関数の零点

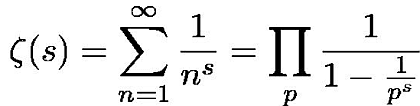
ゼータ関数は上記の関数であり、自然数の s 乗の和を１から無限大に渡ってとる関数である、と同時に素数の s 乗の無限積でもある。ゼータ関数は素数を使って表されることから、素数と密接な関係がある、と認識されていた。

π(x)がゼータ関数の複素零点で表されたことで、リーマンはゼータ関数の零点について研究した。ゼータ関数の零点について実数の零点は判明していたが、複素数の零点は解明されていなかった。リーマンが手計算で４つの複素数の零点を計算したところ、４つとも実部が２分の１だった。このことからリーマンは、ゼータ関数の複素零点はすべて実部が２分の１だろう、と予想した。これがリーマン予想である。リーマン予想は、その後１６３年間数学者を悩ませることとなり、現代数学最大の難問として立ちはだかっている。

複素零点が 0≦Re(s)≦1 の範囲にあることは判明していたが、１８９６年フランスの数学者アダマールが、Re(s)=1 上に複素零点が存在しないことを証明した。ゼータ関数が Re(s)=1/2 の直線に関して対称であることから、複素零点は 0<Re(s)<1 の範囲にあることが証明された。

ボーア・ランダウの定理

１９１３年ボーアとランダウは、

直線Re(s)=1/2を含む細長い長方形の中にゼータ関数の複素零点の存在する確率は、長方形の上を無限大に、下を負の無限大に持ってゆくと１００%に近づく

ということを証明した。ゼータ関数の複素零点は、Re(s)=1/2 の直線の近くにすべて存在する、と言っているのだ。直線 Re(s)=1/2 を含む細長い長方形の中の複素零点を丹念に数え上げて、全部の複素零点の数で割って確率を計算したものである。

リーマン予想の証明にはならなかったが、リーマン予想は正しい、との見通しを多くの数学者に与えてくれた。

ハーディーとリトルウッド

１９２１年、イギリスの数学者ハーディーとリトルウッドは Re(s)=1/2 の上にはゼータ関数の複素零点が無限個存在することを証明した。そして、リーマン予想は証明された、と発表した。

しかし、２人の証明は Re(s)=1/2 の上以外にも複素零点が存在する可能性を潰し切れておらず、リーマン予想問題は振り出しに戻った。

ラマヌジャンなど

その後リーマン予想に取り組んだ数学者を挙げると、インドの天才ラマヌジャンは証明もなしに次々とゼータ関数の数式を書いて人々を驚かせた。「神が数式を与えてくれる」とラマヌジャンは言っていた。リトルウッドはラマヌジャンの才能に注目し、イギリスに呼んで共同研究したのであるが、体の弱かったラマヌジャンは若くして亡くなった。

イギリスの数学者アラン・チューリングは自身が作ったマシンを使って、リーマン予想が間違っていることを示そうとしたが、自殺した。

経済学のノーベル賞学者ジョン・ナッシュはリーマン予想に取り組んでいるときに統合失調症となり、リーマン予想を断念し、経済学に転向してノーベル賞を受賞した。

深リーマン予想

東京工業大学名誉教授黒川信重氏らの推進している深リーマン予想は、ディリクレ L 関数の複素零点を研究してゼータ関数の複素零点が Re(s)=1/2 の上にあることを証明しようとするものである。

コンダクター１のディリクレ L 関数がゼータ関数であり、L 関数の複素零点が Re(s)=1/2 の上にあることを示すことができれば、リーマン予想解決に近づくこととなる。

日本人によってリーマン予想が解決されることを願っている。